试卷题目
1．在3.1415926，
，
√4
，π，√2
，2+√3
，3√27
，| 22 |
| 7 |
√10-2
，0.010010001…(相邻两个1之间增加1个0)这些数中，无理数的个数为( )- A. 5
- B. 4
- C. 3
- D. 2
2．以下列各组数为边长，不能构成直角三角形的是( )
- A. 3，4，5
- B. 1，1，√2
- C. 8，12，13
- D. √2，√3，√5
3．下列变形正确的是( )
- A. √(-16)(-25)=√-16×√-25
- B. √16=
1 4 √16×√=4×1 4 1 2 - C. √(-=)2
1 3 1 3 - D. √252-242=25-24=1
4．已知点A(2x-4，x+2)在坐标轴上，则x的值等于( )
- A. 2或-2
- B. -2
- C. 2
- D. 非上述答案
5．点P在第四象限，且点P到x轴的距离为4，点P到y轴的距离为5，则点P的坐标为( )
- A. (-4，-5)
- B. (4，-5)
- C. (5，4)
- D. (5，-4)
6．对于函数y=-k2x(k是常数，k≠0)，下列说法不正确的是( )
- A. 该函数是正比例函数
- B. 该函数图象过(-，k)
1 k - C. 该函数图象经过二、四象限
- D. y随着x的增大而增大
7．下列说法不正确的是( )
- A. 27的立方根是3
- B. -是
1 2 的平方根1 4 - C. 平方根等于它本身的数只有0
- D. a2的算术平方根是a
8．一次函数y=2x+m的图象过点(a-1，y1)，(a，y2)，(a+1，y3)，则( )
- A. y1＜y2＜y3
- B. y3＜y2＜y1
- C. y2＜y1＜y3
- D. 与m的值有关
9．已知如图是函数y=kx+b的图象，则函数y=-kbx+k的大致图象是( )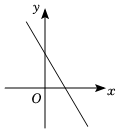
- A.
- B.
- C.
- D.
10．将一组数
…
若
√3
，√6
，3，√12
，√15
，…，√228
按下面的方法进行排列：√3
，√6
，3，√12
，√15
√18
，√21
，√24
，√27
，√30
…
若
√12
的位置记为(1，4)，√24
的位置记为(2，3)，则这组数中最大的有理数的位置记为( )- A. (14，4)
- B. (14，5)
- C. (15，5)
- D. (16，1)
11．-
的倒数是 ．
√6 |
| 2 |
12．若实数m=3，n=4恰好是直角三角形的两条边，则该直角三角形的斜边长为 ．
13．将直线y=x+b沿y轴向下平移2个单位长度，点A(-1，2)关于y轴的对称点落在平移后的直线上，则b的值为 ．
14．如图，已知圆柱底面周长是4dm，圆柱的高为3dm，在圆柱的侧面上，过点A和点C嵌有一圈金属丝，则这圈金属丝的周长最小为 dm．
15．如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D′处．若AB=3，AD=4，则ED的长为 ．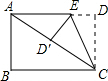
16．笔直的海岸线上依次有A，B，C三个港口，甲船从A港口出发，沿海岸线匀速驶向C港口，1小时后乙船从B港口出发，沿海岸线匀速驶向A港口，两船同时到达目的地．甲船的速度是乙船的1.25倍，甲、乙两船与B港口的距离y(km)与甲船行驶时间x(h)之间的函数关系如图所示．给出下列说法：①A，B港口相距400km；②乙船的速度为80km/h；③B，C港口相距200km；④乙船出发4h时，两船相距220km．其中正确的是 (填序号)．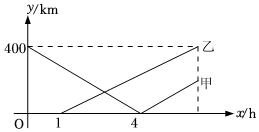
17．计算：
(1)(
(2)
+(
(1)(
√6
-2√15
)×√3
-3√2
；(2)
√20 -√5 |
√5 |
√3
-√2
)2-|2√6
-5|．18．已知|2a+b|与
(1)求6a-13b的平方根和立方根；
(2)解关于x的方程ax2+4b-2=0．
√3b+12
互为相反数．(1)求6a-13b的平方根和立方根；
(2)解关于x的方程ax2+4b-2=0．
19．小明用的练习本可以在甲、乙两个商店买到．已知两个商店的标价都是每本1元．甲的优惠条件是：购买10本以上，从第11本开始按标价的六折卖；乙商店的优惠条件是：从第1本开始就按标价的八折卖．
(1)当购买数量超过10本时，分别写出甲、乙两商店购买本子的费用y(元)与购买数量x(本)之间的关系式；
(2)小明要买15本练习本，到哪个商店购买较省钱？并说明理由．
(3)小明现有28元，最多可买多少本练习本？
(1)当购买数量超过10本时，分别写出甲、乙两商店购买本子的费用y(元)与购买数量x(本)之间的关系式；
(2)小明要买15本练习本，到哪个商店购买较省钱？并说明理由．
(3)小明现有28元，最多可买多少本练习本？
20．如图，在平面直角坐标系中，点B，C的坐标分别为(-a，2a)、(3a，2a)，其中a＞0，点A为BC的中点，若BC=4，解决下列问题：
(1)BC所在直线与x轴的位置关系是 ；
(2)求出a的值，并写出点A，C的坐标；
(3)在y轴上是否存在一点P，使得△PAC的面积等于5？若存在，求P的坐标；若不存在，请说明理由．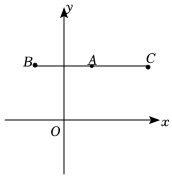
(1)BC所在直线与x轴的位置关系是 ；
(2)求出a的值，并写出点A，C的坐标；
(3)在y轴上是否存在一点P，使得△PAC的面积等于5？若存在，求P的坐标；若不存在，请说明理由．
21．台风是一种自然灾害，它以台风中心为圆心在周围上百千米的范围内形成极端气候，有极强的破坏力，如图，有一台风中心沿东西方向AB由A行驶向B，已知点C为一海港，且点C与直线AB上的两点A，B的距离分别为AC=300km，BC=400km，又AB=500km，以台风中心为圆心周围250km以内为受影响区域．
(1)求∠ACB的度数；
(2)海港C受台风影响吗？为什么？
(3)若台风的速度为20千米/小时，当台风运动到点E处时，海港C刚好受到影响，当台风运动到点F时，海港C刚好不受影响，即CE=CF=250km，则台风影响该海港持续的时间有多长？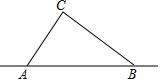
(1)求∠ACB的度数；
(2)海港C受台风影响吗？为什么？
(3)若台风的速度为20千米/小时，当台风运动到点E处时，海港C刚好受到影响，当台风运动到点F时，海港C刚好不受影响，即CE=CF=250km，则台风影响该海港持续的时间有多长？
22．如图，过点A(2，0)的两条直线l1，l2分别交y轴于点B，C，其中点B在原点上方，点C在原点下方，已知AB=
(1)求点B的坐标；
(2)若△ABC的面积为4，求直线l2的解析式．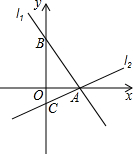
√13
．(1)求点B的坐标；
(2)若△ABC的面积为4，求直线l2的解析式．
扫一扫支付
