试卷题目
1.下列图形中,轴对称图形的个数是( )


- A. 1个
- B. 2个
- C. 3个
- D. 4个
2.下列运算正确的是( )
- A. x•x2=x2
- B. (ab)3=a3b3
- C. x5+x3=x8
- D. a6÷a2=a3
3.等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边为( )
- A. 7cm
- B. 7cm或5cm
- C. 5cm
- D. 3cm
4.如图,红红书上的三角形被墨迹污染了一部分,她根据所学的知识很快就画了一个与书上完全一样的三角形,那么红红画图的依据是( )

- A. SSS
- B. SAS
- C. ASA
- D. AAS
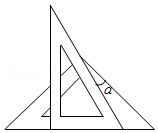
5.一副三角板,按如图所示叠放在一起,则图中∠α的度数为( )

- A. 10°
- B. 15°
- C. 20°
- D. 25°
6.如果把分式
中的x,y都扩大3倍,那么分式的值( )
| 2x |
| 3x-2y |
- A. 扩大3倍
- B. 不变
- C. 缩小3倍
- D. 扩大2倍
7.点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,下列选项正确的是( )
- A. PQ<5
- B. PQ>5
- C. PQ≥5
- D. PQ≤5
8.若x2-2(m-2)x+25是完全平方式,则m的值为( )
- A. 3
- B. -3
- C. 7
- D. -3或7
9.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( )cm2.


- A. 3a+5
- B. 6a+9
- C. 2a2+5a
- D. 6a+15
10.已知甲做360个零件与乙做480个零件所用的时间相同,两人每天共做140个零件,设甲每天做x个零件,根据题意,可列方程为( )
- A. =
360 x 480 140-x - B. =
360 140-x 480 x - C. +
360 x =140480 x - D. -140=
360 x 480 x
11.因式分解:2ab3-2a3b= .
12.当x= 时,分式
的值为0.
| x2-4 |
| x-2 |
13.禽流感病毒的形状一般为球形,直径大约为0.000000102m,该直径用科学记数法表示为 m.
14.有一三角形纸片ABC,∠A=70°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两个纸片均为等腰三角形,则∠C的度数可以是 .
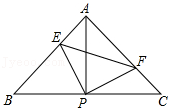
15.如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
①AE=CF;
②△EPF是等腰直角三角形;
③S四边形AEPF=
S△ABC;
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),BE+CF=EF.
上述结论中始终正确的有 (填序号).
①AE=CF;
②△EPF是等腰直角三角形;
③S四边形AEPF=
| 1 |
| 2 |
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),BE+CF=EF.
上述结论中始终正确的有 (填序号).

16.(1)计算:(-2x)3-3x(x-2x2);
(2)分解因式:9x2(x-y)-y2(y-x)+6xy(y-x).
(2)分解因式:9x2(x-y)-y2(y-x)+6xy(y-x).
17.先化简,再求值:
÷(x+2-
),其中x=1.
| x2-6x+9 |
| x-2 |
| 5 |
| x-2 |
18.如图,已知△ABC的顶点分别为A(-2,2),B(-4,5),C(-5,1).
(1)作出△ABC关于x轴对称的图形△A1B1C1,并写出点B1的坐标;
(2)若点P(a,b)是△ABC内部一点,则点P关于y轴对称的点的坐标是 .
(3)在x轴上找一点P,使得AP+CP最小(画出图形,找到点P的位置).

(1)作出△ABC关于x轴对称的图形△A1B1C1,并写出点B1的坐标;
(2)若点P(a,b)是△ABC内部一点,则点P关于y轴对称的点的坐标是 .
(3)在x轴上找一点P,使得AP+CP最小(画出图形,找到点P的位置).

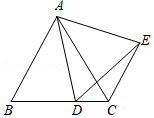
19.如图,△ABC和△ADE均为等边三角形,点D在边BC上,连接CE.
(1)求∠ACE的度数;
(2)猜想线段AC,CD,CE之间的数量关系,并加以证明.
(1)求∠ACE的度数;
(2)猜想线段AC,CD,CE之间的数量关系,并加以证明.

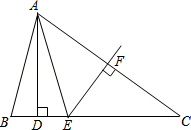
20.如图,在△ABC中,AD⊥BC且BD=DE,EF垂直平分AC,交AC于点F,交BC于点E.
(1)若∠BAE=32°,求∠C的度数;
(2)若AC=6cm,DC=5cm,求△ABC的周长.
(1)若∠BAE=32°,求∠C的度数;
(2)若AC=6cm,DC=5cm,求△ABC的周长.

21.(1)若x+y=8,x2+y2=40,求xy的值;
(2)请直接写出下列问题的答案:
①若2a+b=5,ab=2,则2a-b= ;
②若(4-x)(5-x)=8,则(4-x)2+(5-x)2= .
(2)请直接写出下列问题的答案:
①若2a+b=5,ab=2,则2a-b= ;
②若(4-x)(5-x)=8,则(4-x)2+(5-x)2= .
22.某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值.
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
| 原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
| 餐桌 | a | 270 | 500元 |
| 餐椅 | a-110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值.
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
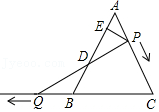
23.如图,△ABC是等边三角形,AB=6,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)证明:在运动过程中,点D是线段PQ的中点;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
(1)证明:在运动过程中,点D是线段PQ的中点;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.






