试卷题目
1.下列长度的三条线段首尾相连能组成三角形的是( )
- A. 5,6,10
- B. 2,5,8
- C. 5,6,11
- D. 3,4,8
2.六多边形的内角和为( )
- A. 180°
- B. 360°
- C. 720°
- D. 1080°
3.在平面直角坐标系xOy中,点P(-3,5)关于y轴对称的点的坐标是( )
- A. (-3,-5)
- B. (3,-5)
- C. (3,5)
- D. (5,-3)
4.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )


- A. CB=CD
- B. ∠BAC=∠DAC
- C. ∠B=∠D=90°
- D. ∠BCA=∠DCA
5.等腰三角形的周长为15,其中一边长为3,则该等腰三角形的底边长为( )
- A. 3
- B. 4
- C. 5
- D. 6
6.在以下三个图形中,根据尺规作图的痕迹,能判断射线AD平分∠BAC的是( )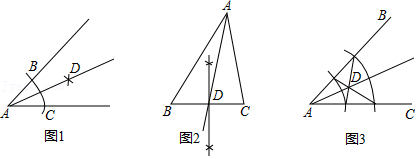

- A. 图2
- B. 图1与图2
- C. 图1与图3
- D. 图2与图3
7.如图所示,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=15,DE=3,AB=6,则AC长是( )
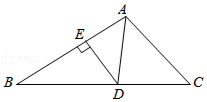

- A. 4
- B. 5
- C. 6
- D. 7
8.如图,已知∠AOB=60°,点P在OA边上,OP=8cm,点M、N在边OB上,PM=PN,若MN=2cm,则OM为( )
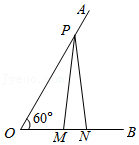

- A. 2cm
- B. 3cm
- C. 4cm
- D. 1cm
9.如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=35°,则∠A+∠C=( )
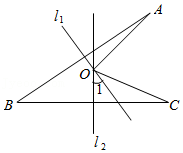

- A. 30°
- B. 40°
- C. 17.5°
- D. 35°
10.如图,等边△ABC中,AD为BC边上的高,点M、N分别在AD、AC上,且AM=CN,连BM、BN,当BM+BN最小时,∠MBN的度数为( )
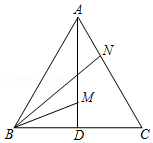

- A. 15°
- B. 22.5°
- C. 30°
- D. 47.5°
11.已知△ABC≌△EFG,若∠A=40°,∠B=60°,则∠G= .
12.如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,则∠DBC= 度.














