试卷题目
1．第24届冬季奥林匹克运动会将于2022年2月4日至2月20日在中国北京市和张家口市联合举办．以下是参选的冬奥会会徽设计的部分图形，其中是轴对称图形的是( )
- A.
- B.
- C.
- D.
2．下列各式是最简分式的是( )
- A.
x2-4y2 (x+2y)2 - B.
x2+y2 x+y - C.
-2xy 9x3 - D.
x2+x x2-1
3．下列计算正确的是( )
- A. x2•x4=x6
- B. a0=1
- C. (2a)3=6a3
- D. m6÷m2=m3
4．下列说法中错误的是( )
- A. 三角形的中线、角平分线、高线都是线段
- B. 边数为n的多边形内角和是(n-2)×180°
- C. 有一个内角是直角的三角形是直角三角形
- D. 三角形的一个外角大于任何一个内角
5．根据下列已知条件，不能画出唯一△ABC的是( )
- A. AB=3，BC=6，CA=8
- B. AB=6，∠B=60°，BC=10
- C. AB=4，BC=3，∠A=30°
- D. ∠A=60°，∠B=45°，AB=4
6．在△ABC中，∠A=∠B=
∠C，则∠C=( )
| 1 |
| 4 |
- A. 70°
- B. 80°
- C. 100°
- D. 120°
7．如图，已知∠ACB=60°，PC=12，点M，N在边CB上，PM=PN．若MN=3，则CM的长为( )
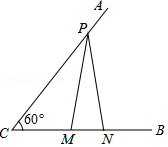
- A. 3
- B. 3.5
- C. 4
- D. 4.5
8．下列等式中，从左到右的变形是因式分解的是( )
- A. m(a+b)=ma+mb
- B. x2+3x+2=(x+1)(x+2)
- C. x2+xy-3=x(x+y)-3
- D. 2x2+2x=2x2(1+)
1 x
9．下列条件中，不能判定直线MN是线段AB(M，N不在AB上)的垂直平分线的是( )
- A. MA=MB，NA=NB
- B. MA=MB，MN⊥AB
- C. MA=NA，MB=NB
- D. MA=MB，MN平分AB
10．若m2+6m+p2是完全平方式，则p的值是( )
- A. 3
- B. -3
- C. ±3
- D. 9
11．如图，任意画一个∠A=60°的△ABC，再分别作△ABC的两条角平分线BE和CD，BE和CD相交于点P，连接AP，有以下结论：①∠BPC=120°；②AP平分∠BAC；③点P到边AB，AC，BC的距离相等；④BD+CE=BC；⑤AD+AE=
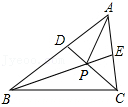
√3
AP，其中错误的个数是( )个．- A. 0
- B. 1
- C. 2
- D. 3
12．在学校组织的秋季登山活动中，某班分成甲、乙两个小组同时开始攀登一座450m高的山，乙组的攀登速度是甲组的1.2倍，乙组到达顶峰所用时间比甲组少15min．如果设甲组的攀登速度为x m/min，那么下面所列方程中正确的是( )
- A. =
450 x +1.2450 x+15 - B. =
450 1.2x -15450 x - C. =1.2×
450 x 450 x+15 - D. =
450 1.2x +15450 x
13．要使分式
有意义，则x的取值范围是 ．
| 3 |
| x2+2 |
14．一个正n边形的每个外角都为60°，则边数n为 ．
15．如图，OM=ON，若用“边边边”证明△CMO≌△CNO，则需要添加的条件是 ．
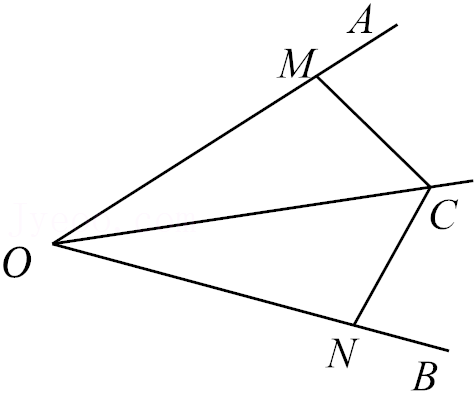
16．若关于x的方程
-5=
无解，则m的值为 ．
| 4x |
| x-2 |
| mx |
| 2-x |
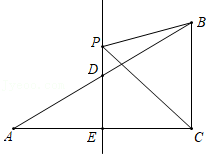
17．如图，在△ABC中，∠ACB=90°，∠A=30°，边AC的垂直平分线DE分别交边AB、AC于点D、E，P为直线DE上一点．若BC=2，则△BCP周长的最小值为 ．
18．如图，点C为线段AE上一动点(不与点A、E重合)，在AE同侧分别作等边△ABC和等边△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ，以下十个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°；⑥CP=CQ；⑦△CPQ为等边三角形；⑧共有2对全等三角形；⑨CO平分∠AOE；⑩CO平分∠BCD恒成立的结论有 (把你认为正确的序号都填上)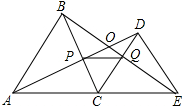
19．(1)分解因式：
①4m2-36；
②2a2b-8ab2+8b3．
(2)解分式方程：
①
-1=
；
②
=
-2．
①4m2-36；
②2a2b-8ab2+8b3．
(2)解分式方程：
①
| x |
| x-2 |
| 6 |
| x2-4 |
②
| 2-x |
| x-3 |
| 1 |
| 3-x |
20．(1)计算：[(x+y)2-(x-y)2]÷(2xy)；
(2)化简求值：
÷(
−1)+1，其中x选取-2，0，1，4中的一个合适的数．
(2)化简求值：
| x2−8x+16 |
| x2+2x |
| 6 |
| x+2 |
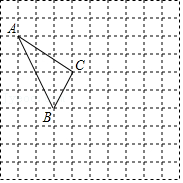
21．在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形(顶点是网格线的交点的三角形)ABC的顶点A，C的坐标分别为(-4，5)，(-1，3)．
(1)请在如图所示的网格平面内作出平面直角坐标系．
(2)请作出△ABC关于y轴对称的△A′B′C′．
(3)求△ABC的面积为 ．
(1)请在如图所示的网格平面内作出平面直角坐标系．
(2)请作出△ABC关于y轴对称的△A′B′C′．
(3)求△ABC的面积为 ．
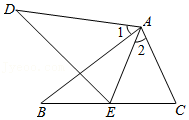
22．如图，DE=BC，∠AED=∠C，∠1=∠2=60°．求证：AE=CE．
23．(1)请写出三个代数式(a+b)2、(a-b)2和ab之间数量关系式 ．
(2)应用上一题的关系式，计算：xy=-3，x-y=4，试求x+y的值．
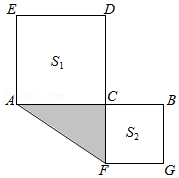
(3)如图：线段AB=10，C点是AB上的一点，分别以AC、BC为边长在AB的异侧做正方形ACDE和正方形CBGF，连接AF；若两个正方形的面积S1+S2=52，求阴影部分△ACF面积．
(2)应用上一题的关系式，计算：xy=-3，x-y=4，试求x+y的值．
(3)如图：线段AB=10，C点是AB上的一点，分别以AC、BC为边长在AB的异侧做正方形ACDE和正方形CBGF，连接AF；若两个正方形的面积S1+S2=52，求阴影部分△ACF面积．
24．2021年10月17日是我国第8个扶贫日，也是第29个国际消除贫困日．为组织开展好扶贫日系列活动，加快脱贫攻坚步伐．我市决定将一批生姜送往外地销售．现有甲、乙两种货车，已知甲种货车比乙种货车每辆车多装20箱生姜，且甲种货车装运1000箱生姜所用车辆与乙种货车装运800箱生姜所用车辆相等．
(1)求甲、乙两种货车每辆车可装多少箱生姜？
(2)如果这批生姜有1535箱，用甲、乙两种汽车共16辆来装运，甲种车辆刚好装满，乙种车辆最后一辆只装了55箱，其它装满，求甲、乙两种货车各有多少辆？
(1)求甲、乙两种货车每辆车可装多少箱生姜？
(2)如果这批生姜有1535箱，用甲、乙两种汽车共16辆来装运，甲种车辆刚好装满，乙种车辆最后一辆只装了55箱，其它装满，求甲、乙两种货车各有多少辆？
