试卷题目
1.若
√3+x
在实数范围内有意义,则x的取值范围是( )- A. x≥3
- B. x>3
- C. x≥-3
- D. x≤-3
2.一个直角三角形的两条直角边边长分别为6和8,则斜边上的高为( )
- A. 4.5
- B. 4.6
- C. 4.8
- D. 5
3.下列说法中错误的是( )
- A. 邻边相等的四边形是正方形
- B. 两条对角线互相垂直且平分的四边形是菱形
- C. 四个角都相等的四边形是矩形
- D. 一组对边平行且相等的四边形是平行四边形
4.如图,直线y=kx+b(k≠0)经过点(-2,4),(-6,0),则不等式kx+b>4的解集为( )


- A. x>-6
- B. x<-6
- C. x>-2
- D. x<-2
5.已知一次函数的图象过点(2,0)和点(1,-1),则这个函数的解析式为( )
- A. y=x-2
- B. y=x+2
- C. y=-x-2
- D. y=-x+2
6.-3,-2,4,x,5,8这六个数的平均数是3,则x的值为( )
- A. 4
- B. 5
- C. 6
- D. 7
7.下列二次根式,化简后能与
√3
合并的是( )- A. √18
- B. √
1 3 - C. √28
- D. √20
8.如图,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF,垂足为G,且AG=AB,则∠EAF=( )
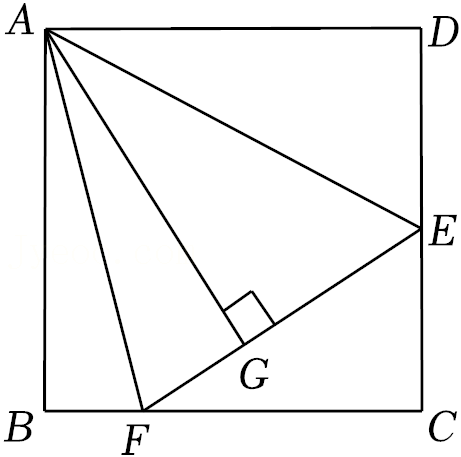

- A. 30°
- B. 45°
- C. 50°
- D. 60°
9.计算(
√3
+√6
)(√3
-√6
)结果等于 .10.若一直角三角形两直角边长分别为6和8,则斜边长为 .
11.已知菱形的两条对角线长为8cm和6cm,那么这个菱形的面积是 .
12.若正方形ABCD的对角线AC的长为4,则该正方形的面积为 .
13.在如图的网格中,每个小正方形的边长为1,A、B、C三点均在正方形格点上,
若AD是△ABC的高,则AD的长为 .
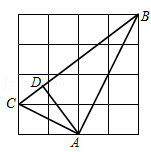
若AD是△ABC的高,则AD的长为 .

14.若平面直角坐标系中,设点P(2,a)在正比例函数y=x的图象上,则点Q(a,3a-5)位于第 象限.
15.甲、乙两人在相同条件下进行射击练习,每人10次射击成绩的平均值都是8环,方差分别为S甲2=2.5,S乙2=1.2,则两人成绩比较稳定的是 (填“甲”或“乙”).
16.如图,在菱形ABCD中,∠ADC=120°,AB=3,点E在BC上,且BE=2EC,BF⊥AE,垂足为F,则BF的值为 .
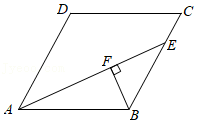

17.(1)计算:3
(2)计算:(2
√3
-6√
+| 1 |
| 3 |
√27
;(2)计算:(2
√3
+3√2
)(2√3
-3√2
).18.如图,在△ABC中,CD⊥AB于点D,AC=20,CD=12,BD=9.求AB与BC的长.
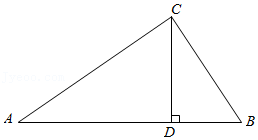

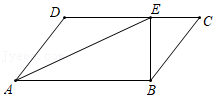
19.如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,AB=16.
(1)求AD的长;
(2)若∠CBE=36°,求∠ADC的度数.
(1)求AD的长;
(2)若∠CBE=36°,求∠ADC的度数.

20.已知在平面直角坐标系xOy中,一次函数的图象经过(3,2)与(-1,-6)两点.
(1)求这个一次函数解析式;
(2)若此一次函数图象与x轴交于点A,与y轴交于点B,求△AOB的面积.
(1)求这个一次函数解析式;
(2)若此一次函数图象与x轴交于点A,与y轴交于点B,求△AOB的面积.
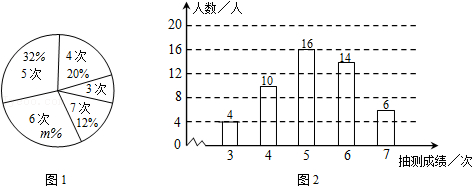
21.为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制出统计图1和图2,请跟进相关信息,解答下列问题:
(1)本次抽测的男生人数为 ,图1中m的值为 ;
(2)求本次抽测的这组数据的平均数、众数和中位数;
(3)若规定引体向上5次以上(含5次)为体能达标,根据样本数据,估计该校350名九年级男生中有多少人体能达标.
(1)本次抽测的男生人数为 ,图1中m的值为 ;
(2)求本次抽测的这组数据的平均数、众数和中位数;
(3)若规定引体向上5次以上(含5次)为体能达标,根据样本数据,估计该校350名九年级男生中有多少人体能达标.

22.如图,已知四边形ABCD为正方形,AB=4
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.

√2
,点E为对角线AC上一动点,连接DE、过点E作EF⊥DE.交BC点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.






