试卷题目
1.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
- A.

- B.

- C.

- D.

2.下列长度的三条线段能组成三角形的是( )
- A. 2,3,4
- B. 3,6,11
- C. 4,6,10
- D. 5,8,14
3.将0.000000301用科学记数法表示应为( )
- A. 3.01×10-10
- B. 3.01×10-7
- C. 301×10-7
- D. 301×10-9
4.下列计算正确的是( )
- A. (a+2)(a-2)=a2-2
- B. (-3a-2)(3a-2)=9a2-4
- C. (a+2)2=a2+2a+4
- D. (a-8)(a-1)=a2-9a+8
5.下列计算正确的是( )
- A. x10÷x2=x5
- B. (x3)2÷(x2)3=x
- C. (15x2y-10xy2)÷5xy=3x-2y
- D. (12x3-6x2+3x)÷3x=4x2-2x
6.如图,下列条件中,不能证明△ABD≌△ACD的是( )
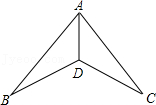

- A. ∠B=∠C,BD=DC
- B. BD=DC,AB=AC
- C. ∠B=∠C,∠BAD=∠CAD
- D. ∠ADB=∠ADC,BD=DC
7.下列计算错误的是( )
- A. a-2÷a5=
1 a7 - B. (a-1b2)3=
b6 a3 - C. ()-2=
b3 a2 1 a4b6 - D. (a-2b2)•(a2b-2)-3=
b8 a8
8.如图①,已知∠AOB,用直尺和圆规作∠AOB的平分线.
如图②,步骤如下:
第一步,以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
第二步,分别以点M,N为圆心,a的长为半径画弧,两弧在∠AOB的内部相交于点C.
第三步,画射线OC.射线OC即为所求.
下列说法正确的是( )

如图②,步骤如下:
第一步,以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
第二步,分别以点M,N为圆心,a的长为半径画弧,两弧在∠AOB的内部相交于点C.
第三步,画射线OC.射线OC即为所求.
下列说法正确的是( )

- A. a>0
- B. a<MN
1 2 - C. a=MN
1 2 - D. a>MN
1 2
9.如图,△ABC的两个外角的平分线相交于点P,则下列结论正确的是( )
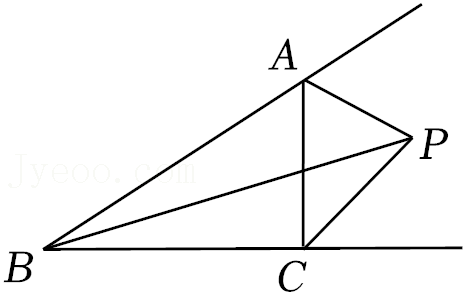

- A. BP平分∠APC
- B. BP平分∠ABC
- C. BA=BC
- D. PA=PC
10.已知abc≠0且a+b+c=0,则a(
+
)+b(
+
)+c(
+
)的值为( )
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| 1 |
| c |
| 1 |
| a |
| 1 |
| b |
- A. 0
- B. 1
- C. -1
- D. -3
11.有一块边长为x米的正方形空地,计划按如图所示的方式去种植草皮(图中阴影部分种植草皮).方式一,如图①,在正方形空地上留两条宽为2a米的互相垂直的路;方式二,如图②,在正方形空地四周各留一块边长为a米的小正方形空地种植树木,现准备用5000元购进草皮.关于哪种方式种植草皮的单价高以及较高的单价是较低的单价的多少倍,正确的说法是( )
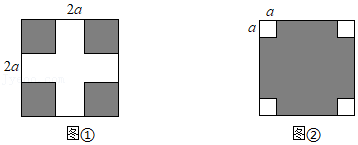

- A. 用方式一比用方式二种植草皮的单价高,且较高的单价是较低的单价的倍
x+2a x-2a - B. 用方式一比用方式二种植草皮的单价高,且较高的单价是较低的单价的倍
x-2a x+2a - C. 用方式二比用方式一种植草皮的单价高,且较高的单价是较低的单价的倍
x+2a x-2a - D. 用方式二比用方式一种植草皮的单价高,且较高的单价是较低的单价的倍
x-2a x+2a
12.如图,等边△ABC中,AD为BC边上的高,点M、N分别在AD、AC上,且AM=CN,连BM、BN,当BM+BN最小时,∠MBN的度数为( )
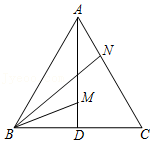

- A. 15°
- B. 22.5°
- C. 30°
- D. 47.5°
13.当x 时,分式
有意义.
| 1 |
| 1-x |
14.计算:24x2y÷(-6xy)= .
15.一个n边形内角和等于1260°,则边数n为 .
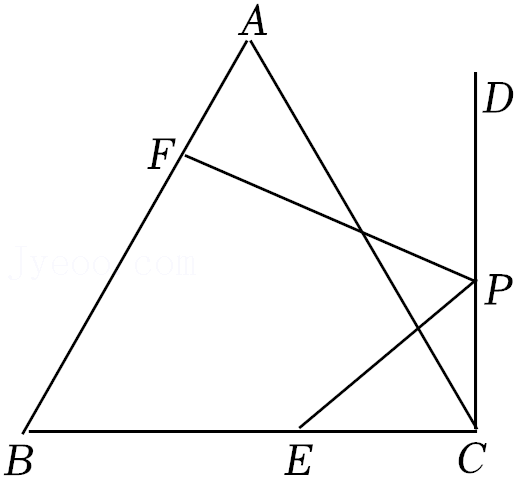
16.如图,点E在等边△ABC的边BC上,BE=12,射线CD⊥BC于点C,点P是射线CD上一动点,点F是线段AB上一动点,当EP+PF的值最小时,BF=14,则AC的长为 .

17.(1)已知x+y=4,xy=3,则x2+y2的值为 .
(2)已知(x+y)2=25,x2+y2=17,则(x-y)2的值为 .
(3)已知x满足(x-2020)2+(2025-x)2=12,则(x-2021)2的值为 .
(2)已知(x+y)2=25,x2+y2=17,则(x-y)2的值为 .
(3)已知x满足(x-2020)2+(2025-x)2=12,则(x-2021)2的值为 .
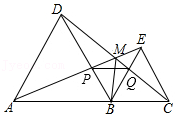
18.如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M、P,CD交BE于点Q,连接PQ,BM.下列结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC.其中结论正确的是 .

19.(1)先化简,再求值x(x-1)+2x(x+1),其中x=1;
(2)计算:(2x+y-6)(2x-y+6).
(2)计算:(2x+y-6)(2x-y+6).
20.计算:
(1)
⋅
;
(2)
+
.
(1)
| 3a+3b |
| 5ab |
| 15a2b |
| a2-b2 |
(2)
| 1 |
| 2p+3q |
| 1 |
| 2p-3q |
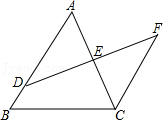
21.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证:△ADE≌△CFE.

22.为抗击新冠肺炎疫情,某公司承担生产8800万个口罩的任务,该公司有A,B两个生产口罩的车间,A车间每天生产的口罩数量是B车间的1.2倍,A,B两车间共同生产一半后,A车间被抽调生产其他急需用品,剩下的全部由B车间单独完成,结果前后共用16天完成.
(1)求A、B两车间每天分别能生产口罩多少万个?
(2)如果A车间每生产1万个口罩可创造利润1.5万元,B车间每生产1万个口罩可创造利润1.2万元,求生产这批口罩该公司共创造利润多少万元?
(1)求A、B两车间每天分别能生产口罩多少万个?
(2)如果A车间每生产1万个口罩可创造利润1.5万元,B车间每生产1万个口罩可创造利润1.2万元,求生产这批口罩该公司共创造利润多少万元?
23.因式分解:
(1)2x3-8x;
(2)(x+3y)2-12xy
(1)2x3-8x;
(2)(x+3y)2-12xy
24.已知等边△ABC.
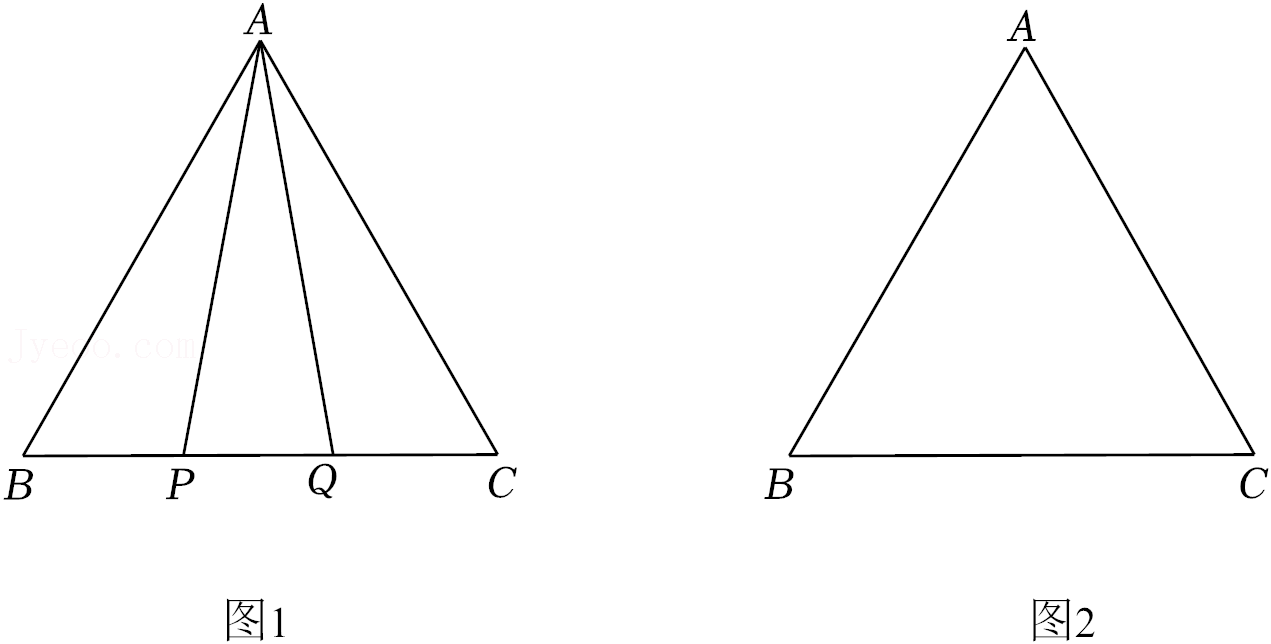
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=15°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM,依题意将图2补全;连接CM,试探究∠PAC和∠PMC的大小关系,并说明理由.
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=15°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM,依题意将图2补全;连接CM,试探究∠PAC和∠PMC的大小关系,并说明理由.

25.已知∠ACB=90°,CD⊥AB,垂足为点D.
(1)如图①,求证∠BCD=∠A;
(2)如图②,E为边BC上一点,且CE=CA,点F是线段CD延长线上一点,连接EF,交AB于点G,若DF=DG,
①求∠EGB的大小;
②求证FD=AD.
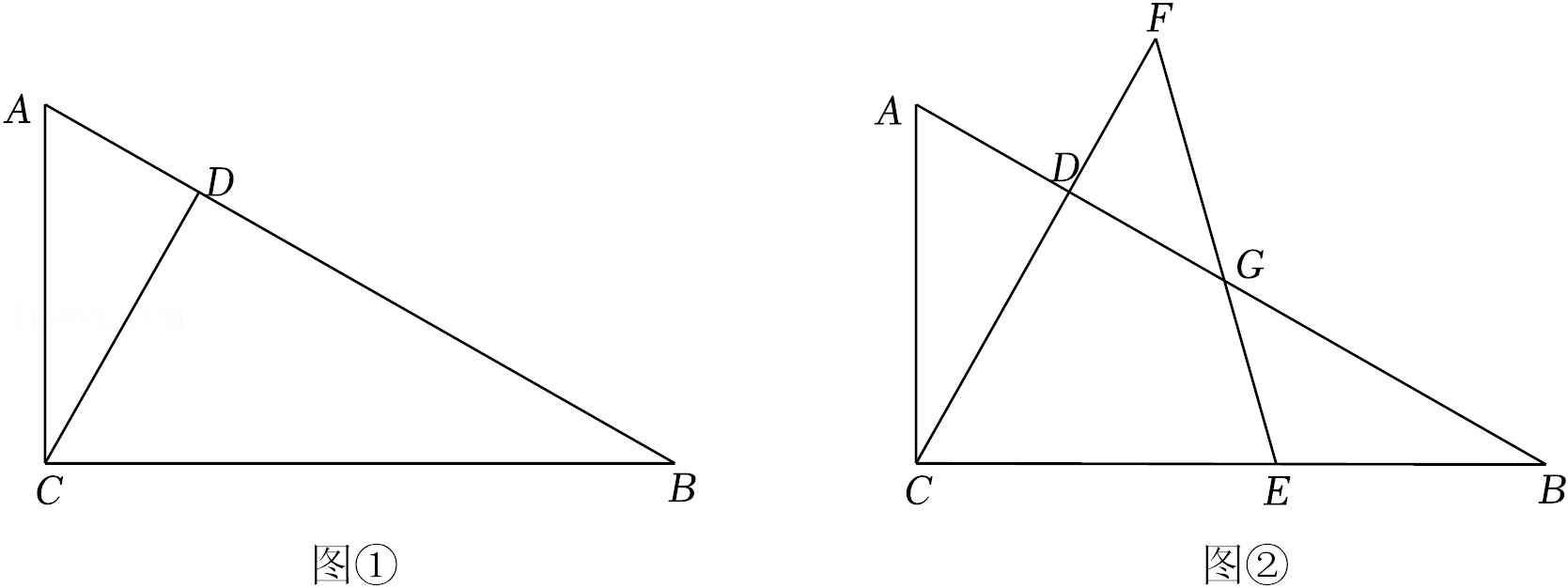
(1)如图①,求证∠BCD=∠A;
(2)如图②,E为边BC上一点,且CE=CA,点F是线段CD延长线上一点,连接EF,交AB于点G,若DF=DG,
①求∠EGB的大小;
②求证FD=AD.






